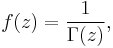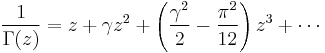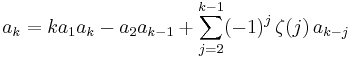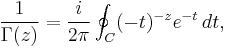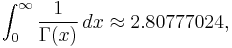Reciprocal Gamma function

In mathematics, the reciprocal Gamma function is the function

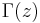f(z) = \frac{1}{\Gamma(z)},

where \Gamma(z) denotes the Gamma function. Since the Gamma function is meromorphic and nonzero everywhere in the complex plane, its reciprocal is an entire function. The reciprocal is sometimes used as a starting point for numerical computation of the Gamma function, and a few software libraries provide it separately from the regular Gamma function.

Karl Weierstrass called the reciprocal Gamma function the "factorielle" and used it in his development of the Weierstrass factorization theorem.

Contents

Taylor series

Taylor series expansion around 0 gives

\frac{1}{\Gamma(z)} = z %2B \gamma z^2 %2B \left(\frac{\gamma^2}{2} - \frac{\pi^2}{12}\right)z^3 %2B \cdots

where \gamma is the Euler–Mascheroni constant. For k > 2, the coefficient ak for the zk term can be computed recursively as

a_k = k a_1 a_k - a_2 a_{k-1} %2B \sum_{j=2}^{k-1} (-1)^j \, \zeta(j) \, a_{k-j}

where ζ(s) is the Riemann zeta function. For small values, this gives the following values:

k a_k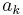
1 1.0000000000000000000000000000000000000000
2 0.5772156649015328606065120900824024310422
3 −0.6558780715202538810770195151453904812798
4 −0.0420026350340952355290039348754298187114
5 0.1665386113822914895017007951021052357178
6 −0.0421977345555443367482083012891873913017
7 −0.0096219715278769735621149216723481989754
8 0.0072189432466630995423950103404465727099
9 −0.0011651675918590651121139710840183886668
10 −0.0002152416741149509728157299630536478065
11 0.0001280502823881161861531986263281643234
12 −0.0000201348547807882386556893914210218184
13 −0.0000012504934821426706573453594738330922
14 0.0000011330272319816958823741296203307449
15 −0.0000002056338416977607103450154130020573
16 0.0000000061160951044814158178624986828553
17 0.0000000050020076444692229300556650480600
18 −0.0000000011812745704870201445881265654365
19 0.0000000001043426711691100510491540332312
20 0.0000000000077822634399050712540499373114
21 −0.0000000000036968056186422057081878158781
22 0.0000000000005100370287454475979015481323
23 −0.0000000000000205832605356650678322242954
24 −0.0000000000000053481225394230179823700173
25 0.0000000000000012267786282382607901588938
26 −0.0000000000000001181259301697458769513765
27 0.0000000000000000011866922547516003325798
28 0.0000000000000000014123806553180317815558
29 −0.0000000000000000002298745684435370206592
30 0.0000000000000000000171440632192733743338

Contour integral representation

An integral representation due to Hermann Hankel is

\frac{1}{\Gamma(z)} = \frac{i}{2\pi} \oint_C (-t)^{-z} e^{-t} \, dt,

where C is a path encircling 0 in the positive direction, beginning at and returning to positive infinity with respect for the branch cut along the positive real axis. According to Schmelzer & Trefethen, numerical evaluation of Hankel's integral is the basis of some of the best methods for computing the Gamma function.

Integral along the real axis

Integration of the reciprocal Gamma function along the positive real axis gives the value

\int_{0}^\infty \frac{1}{\Gamma(x)}\, dx \approx 2.80777024,

which is known as the Fransén–Robinson constant.

See also

References